BTS CG: Corrigé du sujet de mathématiques

 

Voici un corrigé de sujet de BTS CG d'un partiel de mathématiques de 2016. Téléchargez-le gratuitement !

 

Epreuve de 2 heures, coefficient 2

 

Télécharger le document pour voir le corrigé en intégralité.

 

 

Plan du document :

 

I. Exercice 1 (10 points)

 

Partie A - Probabilités conditionnelles

 

Partie B - Loi normale

 

Partie C - Loi binomiale

 

 

II. Exercice 2 (10 points)

 

Partie A - Etude d'une fonction

 

Partie B - Calcul intégral

 

Partie C - Suites numériques

 

 

Exercice 1

 

 

Partie A - Probabilités conditionnelles

 

 

1. P(A) = 0,38, PA(S) = 0,93 et PA(S) = 0,15.

 

 

2. Voici l’arbre donné en annexe complété :

 

 

 

 

 

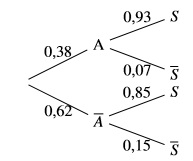
3. P(A∩S) = P(A)×PA(S) = 0,38×0,93≈0,3534.

Donc la probabilité que le client se soit rendu en agence et qu’il ait été satisfait de l’accueil est de 0,3534.

 

 

Télécharger le document pour voir le corrigé en intégralité.

 

 

Partie B - Loi normale

 

 

1. Le coût à estimer est de 10000×1200 = 12000000 euros.

 

2. [800;1600] = [1200−2×200;1200+2×200] on reconnaît (espérance +- 2 écart-type) donc il y a bien 95% des valeurs dans cet intervalle.

 

 

Partie C - Loi binomiale

 

 

1. Notons S : «le dossier choisi a un coût supérieur à 1000 euros». On répète dix fois de manière identique et indépendante une épreuve de Bernoulli de succès S et de paramètre 0,84 donc Y qui compte le nombre de succès S suit une loi binomiale B(10;0,84).

 

 

Télécharger le document pour voir le corrigé en intégralité.

 

 

Exercice 2

 

 

Partie A - Etude d'une fonction

 

 

1. Le nombre d’habitants de la ville le 1er janvier 2015 est f(0).

 

 

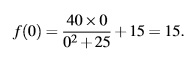
Il y a donc 15 milliers d’habitants de la ville le 1er janvier 2015.

 

 

Partie B - Calcul intégral

 

 

1. Soit x ∈ [0;15] :

 

 

 

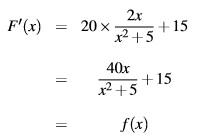
Donc, F est une primitive de f sur [0;15].

 

 

Télécharger le document pour voir le corrigé en intégralité.

 

 

Partie C - Suites numériques

 

 

1. Le nombre d’élève de l’école B augmente de 5% chaque année, donc chaque année le nombre d’élève de l’année d’avant est multiplié par 1,05. Donc le nombre d’élèves de l’école B peut être modélisé par une suite géométrique (bn) de premier terme b0 = 280 et de raison q = 1,05. 

 

 

Télécharger le document pour voir le corrigé en intégralité.